How To Find Square Root Of A Number

Introduction

The relationship between a number and its square root is important to understand. Squaring a number means multiplying it by itself, while finding the square root of a positive number involves finding the number that, when squared, results in the original number. For example, if the square of a number p is q, then the square root of q is equal to p. 

As an example, 2 squared is 4, and the square root of 4 is either +2 or -2.

What is a square of a number?

The square of a number is defined as the product of the number with the number itself. This is represented by a superscript 2 in front of the number. Here are a few examples.

• squared is \(2 \times 2 = {2^2} = 4\)
• 3 square is \(3 \times 3 = {3^2} = 9\)
• 4 square is \(4 \times 4 = {4^2} = 16\)

Square roots

What are square roots?

The square root operation is the inverse of squaring a number. Basically, it is the number which, when multiplied by itself, gives the number whose square root we are trying to find. The square root is operated by the radical symbol \(\sqrt {} \) and the number inside the radical is called the radicand.

Hence, given a number , its square root is represented by \(\sqrt p \)  and if we square \(\sqrt p \) we arrive back at the original number. Thus,

\(\sqrt p  \times \sqrt p  = \sqrt {{p^2}}  = p\)

Square root symbol

The square root function, which is a one-one function, takes a positive number and yields its square root. If it is provided a negative number, the answer is complex.

\(f\left( a \right) = \sqrt a \)

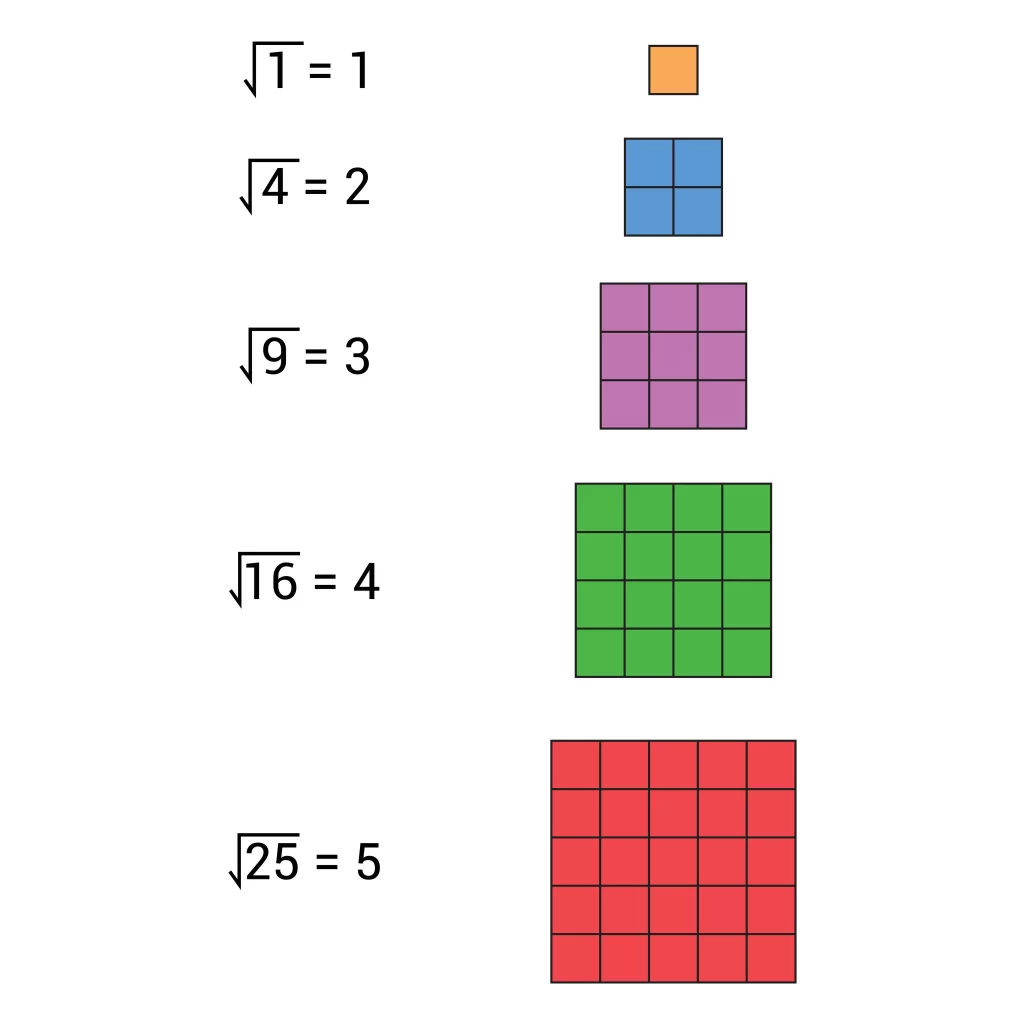
Example: The square root of 4 is equal to \(\sqrt 4  =  \pm 2\)

The square root of 9 is equal to = \(\sqrt 9  =  \pm 3\)

The square root of 16 is equal to = \(\sqrt {16}  =  \pm 4\).

Square roots by prime factorization

We can find the square root of a number by using the prime factorisation method.

1. We start by finding out the prime factors of the number.
2. We then group the same factors into pairs of two.
3. We then take one number each from these pairs and multiply them together. The product we thus obtain is the square root we need.

Example: Find the square root of 36 by using the prime factorization method.

Upon factorising 36, we see that the prime factors come out to be

\(36 = 2 \times 2 \times 3 \times 3\)

We now group the same numbers together

\(36 = \left( {2 \times 2} \right) \times \left( {3 \times 3} \right)\)

And then take one number from each pair. The product thus obtained is the square root. Hence

\(36 = {\left( {2 \times 3} \right)^2} = {6^2}\)

Therefore, the square root of 36 is \( \pm 6\).

Square roots by estimation

In various cases, the perfect square root of a number doesn’t exist and we estimate the nearest value. This can be explained by taking the example of 24.

1. Start by finding the nearest perfect squares to 24. These are 25 and 16, whose square roots are 4 and 5.
2. Since \({5^2}\)  is closer to 24, we increase 4 to 4.5 and check again.
3. Again, \({4^2} = 20.25,So\;{5^2}\) is still closer to 24. We adjust again and go from 4.5 to 4.8.
4. This way, we continue till a close enough estimate has been made. In this case, it comes out to be 4.8989

Also read: How to Find Cube Root of a Number

Square roots by Long division method

It is a method used to find the square roots of large numbers by dividing them into parts and getting the exact value of the square root of the number.

Example: Find the square root of 150 using the long division method?

To obtain the square root of a number using long division:

1. Group the digits of the number into pairs starting from the rightmost digit. This is done by placing bars on top of the groups for easy identification.
2. Find the largest perfect square less than or equal to the leftmost pair (which is 1 here) and use its square root as the divisor and quotient (both come out to be 1). Divide the leftmost pair (1 here) by the divisor, and bring down the next pair of digits (50 here). 
3. Bring the last digit of the quotient (1 here) to the divisor (1 again) and using the sum of these two numbers (1+1=2). Now try to find the largest two digit number that starts with 2 and doubling which, will give us a number below the number we have brought down (50 here).
4. Continue the process in this way and add a decimal point in the quotient and zeroes in the dividend if required untill a desired accuracy is reached. The final quotient will become our square root.

The following table better demonstrates this:

Hence, the square root of 150 is equal to 12.247

Solved Examples

1. Find the square root of 144 via prime factorization.

When we factorise 144, we arrive at the following equation

\(144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3\)

We group these factors into pairs

\(144 = \left( {2 \times 2} \right) \times \left( {2 \times 2} \right) \times \left( {3 \times 3} \right)\)

Then take one factor from each pair.

\(144 = 2 \times 2 \times 3\)

Hence, 12 is the square root of 144.

2. Estimate the square root of 30.

The nearest perfect squares are 25 and 36 and therefore, the square root of 30 must lie between 5 and 6. Since \({5.5^2} = 30.25\), the square root of 30 is very close to 5.5. We now try the guess 5.4, whose square is 29.16. To get better accuracy, let us go up to 5.45, whose square is 29.7025. Continuing this way, we get the desired answer as 5.4772.

Summary

This article discussed the following concepts:

1. What is meant by the square and square root of a number?
2. How square roots are represented.
3. Various ways of finding square roots of a number. These included prime factorization, estimation, and long division methods.

 

Frequently Asked Questions

1.What are the methods used in finding the square root of a decimal number?

The square root of a decimal number may be found via long-division or estimation methods.

2. When is prime factorization useful?

Prime factorization is only useful when the given number is a perfect square. Otherwise, it fails.

3. What are perfect squares?

Perfect squares are those numbers whose square roots are whole numbers, rather than decimal numbers.

4. How do we find square roots of numbers which aren’t perfect squares?

Estimation and long division methods can aid us in such scenarios.