Introduction
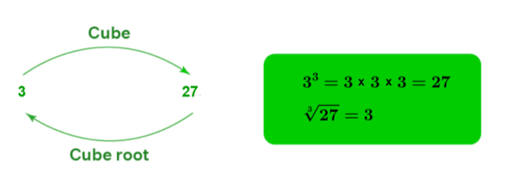
When a number (n) is multiplied three times, the result is known as the cube of that number. As a result, the cube of the number (n) is \({n^3}\) or n-cubed. Select the number 4 as an example. We already know that . As a result, 64 is known as the cube of 4. The cube root of a number, on the other hand, is the inverse of the cube of a number and is denoted by \(\sqrt[3]{{}}\) In the same example, 4 is called the cube root of 64. Let’s go ahead and learn more about the numbers’ cubes and cube roots.
What is a cube of a number?
A cube number is an outcome of multiplying an integer by the same integer three times. They also go by the name “perfect cubes,” or cube numbers. For example, \(4 \times 4 \times 4 = {4^3} = 64\). A number multiplied by the same number three times is called a cube number, or a number with the exponential power of three. Because a negative number produces a negative number when it is multiplied by the same negative number three times, cube numbers of positive numbers are positive, while cube numbers of negative numbers are negative. For example, \({\left( { – 6} \right)^3}\)
In geometry, a cube’s volume is equal to the product of its length, breadth, and height. The length, breadth, and height are all equal inside the cube because it is a cube. The cube’s volume is therefore equal to , which is its length, height, and width. This implies that a cube’s volume is a cube number.
What are the cube roots?
When we hear the word cube root, the first two words that come to mind are cube and roots. In this sense, the concepts are somewhat similar; “root” refers to the primary source of origin. As a result, we only need to consider “which number’s cube must be chosen to get the given number.”
In a nutshell, the cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.
Cube roots by prime factorization
The prime factorization method can be used to calculate the cube root of a number. Begin by determining the prime factorization of a given number to find its cube root. Then, divide the obtained factors into groups, each having three identical factors. Then, to get the answer, eliminate the symbol of the cube root and multiply the factors. If any factor remains that cannot be equally divided into sets of three, the given number isn’t a perfect cube, and we cannot determine its cube root.
Example: How to determine the cube root of 10648.
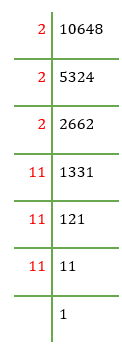
\(\begin{array}{l}\sqrt[3]{{10648}} = \sqrt[3]{{2 \times 2 \times 2 \times 11 \times \times 11 \times \times 11}}\\\;\;\;\;\;\;\;\;\;\;\; = 2 \times 11 = 22\end{array}\)
Cube roots by estimation
If a number has several digits, it will be difficult for you to use the prime factorization and long division methods to compute the square and cube roots of the number. You will thus attempt to estimate the cube root and square root values for these numbers. Factorization becomes challenging as the number of digits rises. Estimating a square root and a cube root in such circumstances is a wise move.
The following step can be used to determine a large integer’s cube root using the estimation method if it is claimed that the provided number is a perfect cube.
Step 1: Starting with the rightmost digit, create a group of three digits starting with any cube number, such as 19683, whose cube root needs to be found.
Step 2: The unit’s digit of the necessary cube root will be provided by the first group. Since the unit digit is 3, we need to find the cube root of the cube which also has unit digit 3, i.e., \({7^3} = 343\) has unit digit 3. Hence, our unit digit for the cube root is 7.
Step 3: Now take the second group, i.e., 19, and find the cube root that is just smaller than 19 ( second group ).
\({2^3} < 19 < {3^3}\).
8 or is just smaller than 19 hence our tenths place digit is 2.
Hence, the cube root of 19683 is equal to
\(\sqrt {19683} = 27\)
Solved examples
Example 1: Determine the following:
1. \(\sqrt[3]{{729}}\)
Solution: We will be using the prime factorization method.
From it, we will get
Now operate both the sides under the cube root.
\(\begin{array}{l}\sqrt[3]{{729}} = \sqrt[3]{{3 \times 3 \times 3 \times 3 \times 3 \times 3}}\\\;\sqrt[3]{{729}} = 3 \times 3 = 9\end{array}\)
2. \(\sqrt[3]{{1728}}\)
Solution: We will be using the prime factorization method.
From it, we will get
Now operate both the sides under the cube root.
\(\begin{array}{l}\sqrt[3]{{1728}} = \sqrt[3]{{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3}}\\\;\sqrt[3]{{1728}} = 2 \times 2 \times 3 = 12\end{array}\)
3. \(\sqrt[3]{{2744}}\)
Solution: We will be using the prime factorization method.
From it, we will get
Now operate both the sides under the cube root.
\(\begin{array}{l}\sqrt[3]{{2744}} = \sqrt[3]{{2 \times 2 \times 2 \times 7 \times 7 \times 7}}\\\;\sqrt[3]{{2744}}\; = 2 \times 7 = 14\end{array}\)
Example 2: Determine the cube root of 59319 using estimation.
Solution:
The given number is 59319
First, we have to make the group of three from the right side. So we have the first group (319) and the second group (59).
To find the unit digit of the cube root, we have to find the cube that has the unit digit equal to the unit digit of the first group.
\({9^3} = 729\)
The cube of 9 has the unit digit 9, so our unit digit of the cube root is 9.
Now take the second group 59 and find the cube root that is just smaller than 59.
\({3^3} < 59 < {4^3}\).
27 or \({3^3}\) is just smaller than 59, hence our tenth place digit is 3.
Hence, the cube root of 59319 is equal to
\(\sqrt {59319} = 39\)
Summary
When we hear the word cube root, the first two words that come to mind are cube and roots. In this sense, the concepts are somewhat similar; “root” refers to the primary source of origin. As a result, we only need to consider “which number’s cube must be chosen to get the given number.” The cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.
When we say n is a cube root of m, then we can denote it as \(\sqrt[3]{m} = n\), with a small 3 written on the top left of the sign. The radical sign \(\sqrt[3]{{}}\) is used as a cube root symbol for any number. Another way to express cube root is to write 1/3 as a number’s exponent. In cube roots, negative values are allowed, unlike in square roots,
For example, \(\sqrt[3]{{ – 216}} = – 6\)
If you’re struggling with the concept of finding the cube root of a number, don’t worry – we’re here to help! Check out our video lesson no. 15 in 88guru’s online Math tuition for 8th class students.
Frequently Asked Questions
1. State the definition of cube root.
Ans: The cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.
2. How is a cube root different from a square root?
Ans: A cube root is a number that when cubed yields the wanted number, whereas a square root yields the wanted number when squared. Furthermore, in cube roots, negative values are allowed, unlike in square roots.
3. What is the name of the method used for finding cube roots?
Ans: The prime factorization method is used to calculate the cube root of a number.
4. What is the cube root of 125?
Ans: 125 is a perfect cube, and 5 is the cube root of 125.
5. How Can a Cube Root Be Simplified?
Ans: The prime factorization method can be used to simplify the cube root. First, prime factorize the given number and then extract the common factors in groups of three. To find the answer, multiply these common factors by two.
 Mission Statement
Mission Statement
“Empower every student to achieve full potential”
88Guru has been established with the social objective of making quality video-based learning material available to all Indian students. Technology, Connectivity and Social Media are rapidly changing the world of Education and we wish to lead the transformation of the tuition industry in India.
88Guru is the perfect complement to the current tuition model. 88Guru creates a wonderful opportunity for children and parents to bond while engaging in a valuable learning activity. It also provides the complete curriculum at your fingertips for those moments when you need some help at short notice. We believe that this mode of tuition could be transformational, adding hours to a child's day while providing complete control over the learning process.
Every course is taught by the best teachers from India's top schools and conducted in an engaging manner to keep students involved. The e-learning process consists of video-based instructions, computer-graded assignments, and a dashboard which allows the student and parent to track progress.


