Introduction
Fractions generally do not have any restriction on the numbers that appear in their numerator or denominator, apart from the fact that the denominator can be zero. However, fractions whose denominators are powers of 10 belong to a specific class of fractions known as decimal fractions. These fractions are most often encountered in scientific calculations, architectural designing, fitness parameters, etc. Hence, their uses are vast in number, and we must have a functional understanding of such fractions. This article is aimed at providing the same.
Decimal Fractions
The word “decimal fractions” is made up of two mathematical words, viz. “decimal” and “fractions”. Separately, we are aware that “decimal” means something that is connected to the value 10 (deci means 10), and that “fraction” refers to ratios. Together, decimal fractions are those fractions wherein, the denominator is a power of 10. Some easy examples of decimal fractions are 21/10, 53/100, 34/1000. As we will soon see, decimal fractions have some special properties that allow us to classify them together.
Just like other fractions, decimal fractions can also be represented in the form p/q. The only difference is that this time, q is necessarily a power of 10. In the figure below, we graphically represent the difference between decimal and non-decimal fractions.
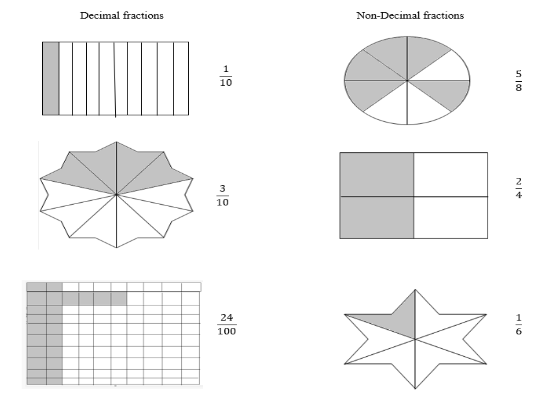
Place value of Decimal Fractions
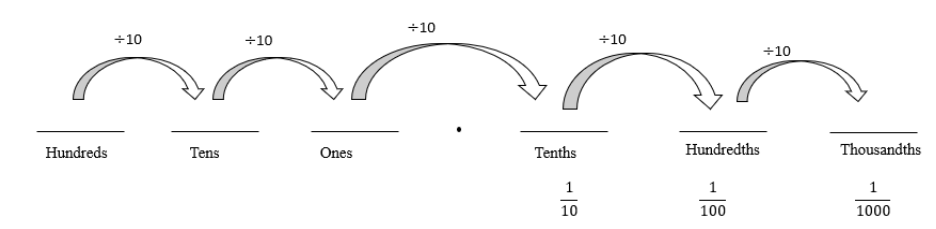
When studying whole numbers, we have come across place values, which increase towards the left. The right-most digit has the place value of one, then ten, then hundred, and so on. Since decimal fractions contain powers of 10 in the denominator, their value decreases if the power of 10 decreases.
Take a look at the figure below and notice how with increasing power of 10, the fraction becomes smaller and smaller. We start with tenths, then we get hundredths, then thousandths, and so on. By tenths, we mean one in ten portions and thus, one hundredth is much smaller than one tenth.
Operations on Decimal Fractions
All fractions can undergo addition, subtraction, multiplication, and division, and decimal fractions are no different. The rules to be followed remain the same here. However, since the denominator is always a power of 10 only, calculations are simpler this time around.
Conversion to Decimal Fractions
The conversion of any number to a decimal fraction is an easy task and we will discuss it here.
First, we have the simplest case of a number carrying a decimal point. Given such a number, we simply need to remove the decimal point and put as many powers of 10 in the denominator as there were digits after the decimal points. For example, 3.14 is simply 314/10² = 314/100.
Next, if we are given a fraction, we check the denominator and see if it can be directly converted to a power of 10 by multiplication with a suitable factor. For instance, given the number 13/20, we see that we can multiply 20 with 5 to get 100. Thus, we multiply the numerator and denominator with 5 to get 65/100, which is the decimal fraction form of 13/20.
If that is also not possible, we simply divide the fraction to get a decimal number and convert it into a decimal fraction as previously stated. For example, 10/21 can’t be directly converted to a decimal fraction. Thus,
10/21 = 0.48 (approximately)
And 0.48 = 48/100.
Addition of Decimal Fractions
The addition of decimal fractions can be achieved via two ways:
- Convert to a decimal number and add the decimal numbers.
For example, given 7/10 and 89/100, we get the decimal forms as 0.7 and 0.89. Now 0.7+0.89 = 1.59 = 159/100. - Make the denominators of the two numbers same and then add.
Taking the same example as before, 7/10 and 89/100 can be given the same denominator if we multiply and divide the first fraction by 10. Thus, we have 7/10 = 70/100. Now, we can easily add these numbers to get 70/100 + 89/100 = 159/100. As expected, the answer is the same.
Subtraction of Decimal Fractions
The subtraction of decimal fractions follows exactly the same procedure as addition. Thus, 62/100 – 1/10 = 0.62-0.1 = 0.52 = 52/100. The same result may be achieved by making the denominators the same.
Multiplication of Decimal Fractions
Multiplication for decimal fractions follows the same rules as normal fractions. Thus, the numerator is multiplied with the numerator and the denominator with the denominator. Since the denominators are both powers of 10, we just add their powers to get the product for the denominator. Thus, 9/10 ✕ 178/1000 = (9 ✕ 178) / (10 ✕ 1000) = 1602/10000.
Division of Decimal Fractions
Just like other operations, division of decimal fractions also follows the same procedure. However, since the denominators of the two fractions are both powers of 10, we can easily subtract the powers for the denominators. In general, to divide two fractions, we first write the reciprocal/inverse of the second fraction and multiply it with the first one.
For example, given 49/100 and 134/1000, we have
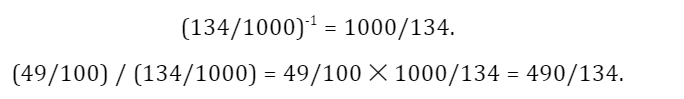
Types of Decimal Fractions
Decimal fractions can be categorised into three types, which are listed below:
- Terminating decimals: If the decimal number form of the fraction ends after a finite number of digits, the fraction is said to be terminating. For example, 49/100 = 0.49, 45/10 = 4.5, etc.
- Non-terminating repeating decimals: These are decimal fractions which, when represented in decimal form, repeat their digits indefinitely. For example, 2/11 = 0.1818181818…
- Non-terminating non-repeating decimals: These are irrational numbers whose decimal expansion does not end and does not repeat. The best example is the approximation for π = 22/7 = 3.1415926535897…
Solved Examples on Decimal Fractions
1. Convert 5/16 to a decimal fraction
We see that the denominator is equal to 16. If we multiply 16 with 625, we get 16 ✕ 625 = 10000. Thus,
5/16 = (5✕625) / (16✕625) = 3125/10000.
2. If a tank contains 4.89 litres of oil and 2.62 litres are removed from it, how many litres are left. Use decimal fractions.
Our task is to first convert these numbers to decimal fractions and then subtract. Hence,
4.89 = 489/100
2.62 = 262/100
489 / 100 – 262 / 100 = (489-262) / 100 = 227/100 = 2.27
Hence, the tank now contains 2.27 litres of oil.
3. The product of two numbers is 111.09 and one of them is 6.9. Find the other number.
Let us again convert the numbers to decimal fractions to get
111.09 = 11109/100
6.9 = 69/10 = 690/100
To find the unknown number, we will need to divide 11109/100 with 690/100. Hence, if the unknown number is x, we have
x = (11109/100) / (690/100)
X = 11109/100 ✕ 100/690 = 11109/690 = 16.1
Thus, the other number is 16.1
Summary
This article briefly summarised the concepts of decimal fractions and algebraic operations related to these fractions. We learnt that decimal fractions are a special class of fractions whose denominators are powers of 10 only. We further learnt how to represent any number in the form of a decimal fraction. Hence, this article serves as a useful guide for understanding the concept of decimal fractions.
Frequently Asked Questions
1. What is the difference between decimal fractions and percentages?
Decimal fractions can contain any power of 10 in their denominator. However, percentages are always calculated out of 100 and thus, the denominator is necessarily 100.
2. How do we round off decimal numbers?
Rounding off decimal numbers is similar to rounding off whole numbers. We start with the last digits and check whether it is greater than equal to 5. If so, we increase the second-last digit by 1 and drop the last digit. If not, we simply drop the last digit without incrementing the second-last one. This process is continued till the desired number of digits are reached.
3. Are all rational numbers decimal fractions?
All rational numbers can be represented in the form of decimal fractions. However, this does not mean they are decimal fractions. But the converse is true. All decimal fractions are necessarily rational numbers.
4. Do decimal fractions obey commutative, additive, or distributive laws?
Yes. Decimal fractions obey all the laws that govern normal fractions.
 Mission Statement
Mission Statement
“Empower every student to achieve full potential”
88Guru has been established with the social objective of making quality video-based learning material available to all Indian students. Technology, Connectivity and Social Media are rapidly changing the world of Education and we wish to lead the transformation of the tuition industry in India.
88Guru is the perfect complement to the current tuition model. 88Guru creates a wonderful opportunity for children and parents to bond while engaging in a valuable learning activity. It also provides the complete curriculum at your fingertips for those moments when you need some help at short notice. We believe that this mode of tuition could be transformational, adding hours to a child's day while providing complete control over the learning process.
Every course is taught by the best teachers from India's top schools and conducted in an engaging manner to keep students involved. The e-learning process consists of video-based instructions, computer-graded assignments, and a dashboard which allows the student and parent to track progress.


