Adiabatic Processes Derivation

Introduction

In thermodynamics, we explore various variables, including temperature, pressure, volume, entropy, heat, etc. These variables form the foundation for thermodynamic processes, which may be classified into isothermal, isobaric, adiabatic processes, etc. 

In an adiabatic process, thermodynamic variables can change value so long as no exchange of heat occurs. There are two critical requirements for such a process to occur:

1. The walls of the piston must be sealed to prevent heat exchange between the system and the environment. 
2. The process of compression or expansion must be completed rapidly.

 

Adiabatic processes

Derivation of adiabatic process formula

Adiabatic Relations between P, V, and T

The first law of thermodynamics gives rise to the conservation of energy, forbidding it from being created or destroyed.

 

Adiabatic relation between P and V

As per the first law, the change in heat energy is equal to the sum of the change in internal energy and the work done. That is,

Adiabatic relation between P and T

We again start with a mole of an ideal gas. Then, from the ideal gas equation,

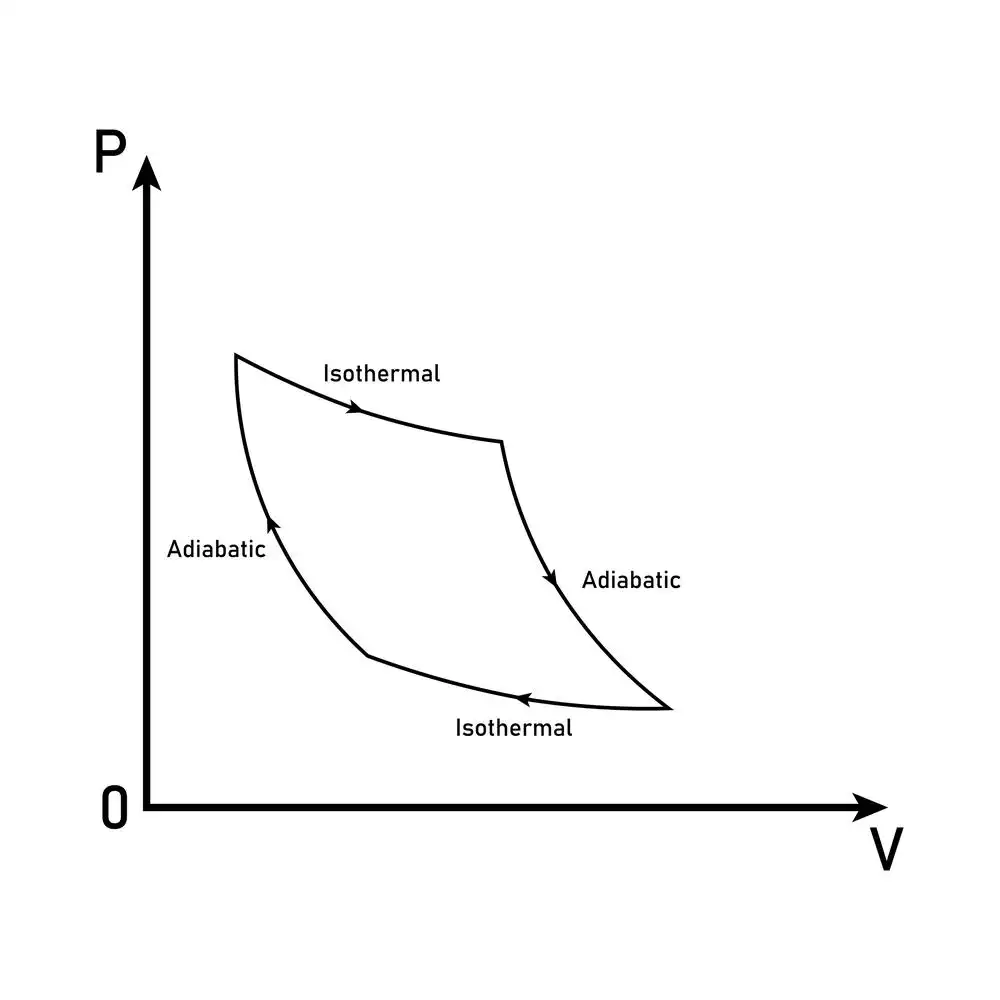
 Adiabatic relation between V and T:

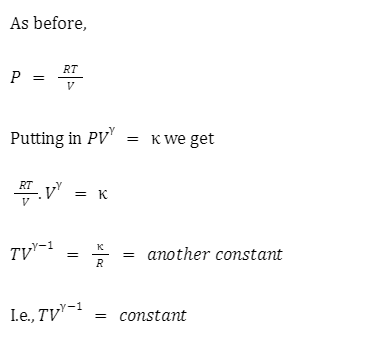
Examples of Adiabatic Process

1. An ice-box prevents heat from entering the system and thus, is an adiabatic system.
2. Hot water kept in a thermal flask is an example of an adiabatic system.
3. When warm air rises from the Earth’s surface, it expands adiabatically. As a result, the water vapour cools and condenses into water droplets forming a cloud.
4. A gas being compressed or undergoing rapid expansion is an adiabatic process since there isn’t enough time for heat exchange to occur.

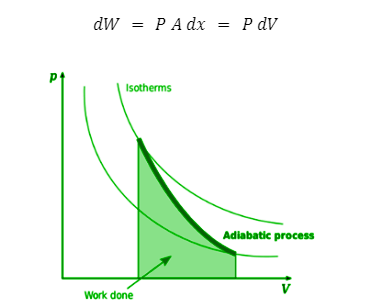
Adiabatic Expansion

Adiabatic expansion is defined as a perfect condition for a confined system, where the pressure remains constant, and the temperature decreases.

Work done in an adiabatic expansion process

To derive the formula for work done, we start with a closed cylinder that contains n moles of an ideal gas. If P represents the pressure of this gas, and the piston in the cylinder moves up by a distance x, the work done by the gas may be written as:

Adiabatic work done

Description: The work done in an adiabatic process is the area under the curve

Here, A represents the cross-sectional area of the piston and dV = Adx is the increase in volume due to the piston’s movement. Suppose the initial and final stages of the system are \(\;({{\bf{P}}_1},{{\bf{V}}_1},{{\bf{T}}_1}){\bf{and}}({{\bf{P}}_2},{{\bf{V}}_2},{{\bf{T}}_3})\), respectively. Then the total work done is:

Shown above is the equation for the work done in an adiabatic process for a system consisting of n moles of an ideal gas. When the gas does work during adiabatic expansion, the work done is positive and the temperature of the gas decreases\(\left( {{T_2} < {T_1}} \right)\). Conversely, when work is done on the gas during adiabatic compression, the work done is negative and the temperature of the gas increases \(\left( {{T_2} > {T_1}} \right)\)

.

Adiabatic Compression

Adiabatic compression is a process wherein, a system undergoes compression without exchange of heat with its surroundings. It leads to an increase in temperature and a decrease in volume.

Adiabatic-reversible and irreversible process

Reversible adiabatic process: An adiabatic process is said to be reversible if the system can revert back to its original state after the process has taken place. Such a process isn’t possible in nature.

Irreversible process: An irreversible adiabatic process is one that cannot be reversed. It is accompanied by an increase in entropy and all real adiabatic processes are irreversible.

Conclusion

An adiabatic process is characterized by changes in the pressure, volume, and temperature of a system, but with no exchange of heat taking place between the system and its surroundings. For an adiabatic process to occur, certain conditions must be met: the walls of the container must be insulated, and the speed of compression or expansion must be rapid enough to prevent heat exchange.

For an adiabatic process, the relation between pressure and volume is \(P{V^\gamma } = \kappa \). This equation may be rewritten in terms of pressure and temperature as\({P^{1 – \gamma }}{T^\gamma } = {\rm{constant}}\), or in terms of volume and temperature as \({\rm{T}}{{\rm{V}}^{\gamma  – 1}} = {\rm{constant}}\)

The work done for an adiabatic process is given by the following expression:

Wadia = nR-1 T1 – T2

 

Frequently Asked Questions

1. The adiabatic process occurs at rapid rate. Explain why?

If the process were to occur slowly, it would give the system time to exchange heat, which would make the process non-adiabatic.

2. During the Adiabatic expansion, the temperature of gas gets lowered. why?

During adiabatic expansion, work is done by the system, causing a decrease in its internal energy. This lowers its temperature.

3.Difference between the Adiabatic and Isothermal processes?

4. Is the work done in an Adiabatic process change depending on which physical quantity?

5.  In adiabatic expansion, how the internal energy is affected?