Congruence of Angles

Introduction

In geometry, an angle is made when two rays are joined at the same location. The common point is referred to as the node or vertex, while the two rays are known as the arms of the angle. We use the symbol “\(\angle \)” to represent an angle. The word “angle” has its roots in the Latin word “Angulus”, before talking about congruent angles, let’s define the term. In geometry, two figures are said to be congruent if their size and shapes are the same. That suggests that they will completely overlap if we stack one figure on top of the other. These figures may be line segments, polygons, angles, or 3D objects.

Congruent Angle Construction

Corresponding angles are always congruent on congruent figures. Two situations are there while learning about the construction of congruent angles in geometry. They are
• Any measurement can be used to create two congruent angles.
• making a new angle that is comparable to the one already there
Let’s look at two angles that are congruent with each other.

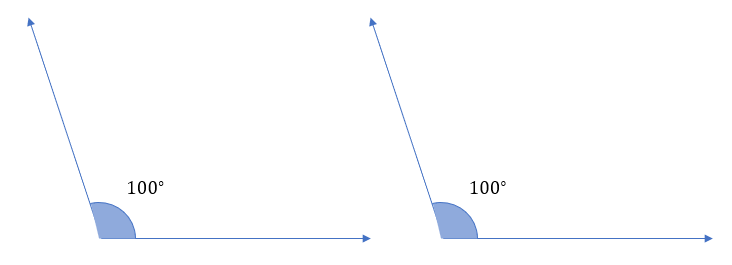
In the figure above, the angles are equal in size (\({100^\circ }\) each). They might completely encircle one another. As a result, both of the above angles satisfy the concept of congruent angles.

The symbol \(\angle 1 \cong \angle 2\) represents the congruence of two angles.

Angle Congruence Theorems

Many theorems are built on the concept of congruent angles. The congruent angles theorem allows us to easily assess whether two angles are congruent or not. The following are the theorems:

• The vertical angle theorem
• The corresponding-angles theorem
• The alternate-angles theorem
• Congruent supplement theorem
• Congruent complements theorem

Let’s talk about how these theorems are stated. Different theorems can be used to demonstrate if two or more angles are congruent. The following are the theorems:

The vertical opposite angle theorem

If two lines intersect each other, then the vertically opposite angles are equal.

Congruent Complements Theorem

The next theorem, the congruent complements theorem, states that if two angles are complements of the same angle, then the two angles are congruent.

Congruent Supplements Theorem

According to the Congruent Supplements Theorem, two angles are congruent if they are supplements of the same angle.

The alternate interior angles theorem

This theorem states that the alternate interior angles are equivalent if a transversal intersects two parallel lines.

The alternate exterior angles theorem

This theorem states that the angles formed on the outer side of the parallel lines and opposite sides of the transversal, when a transversal joins two parallel lines, have to be equivalent.

The theorem of Corresponding Angles

If a transversal meets two parallel lines, the corresponding angles that result are congruent.

Summary

This article showed us that a pair of angles cannot be congruent unless their measurements are equal. The statements of congruence of vertical angles theorem, corresponding angles theorem, alternate angles theorem, congruent supplements theorem, and congruent complements theorem were the next ideas we learned. We next discussed a few examples of congruent angles. We also learned how the angles are congruent based on these theorems. When two unknown angles are regarded as congruent, as well as how to calculate an angle’s measure, were both covered. Finally, we solved several cases that illustrated the concept of congruence of angles.

1. What is an angle? What are the measuring units of angles, and what is the relation between them?

Ans. An angle is the elevation of one line from another. Angles are measured in two main unit systems, i.e., the degree system and the radian system. The degree system has 2 sub-divisions, minutes and seconds. 1 complete circle is 360 degrees, 1 degree has 60 minutes and 1 minute has 60 seconds, the degree system angles are always represented by whole numbers and any fractional part is moved on to the next subdivision. Whereas the radian system has no subdivisions and can be represented in whole numbers, fractions and decimals. In the radian system, 1 complete circle is \(2\pi {\text{ rad}}\).

\[{360^\circ } = 2\pi {\text{ rad}}\]

\[{1^\circ } = \frac{\pi }{{180}}{\text{ rad}}\]

\[1{\text{ rad}} = {\frac{{180}}{\pi }^\circ }\]

2.What do you mean by congruent angles?

Ans. An angle is said to be congruent to another angle if the two angles are equal in measure.

3.Are the following two angles congruent?

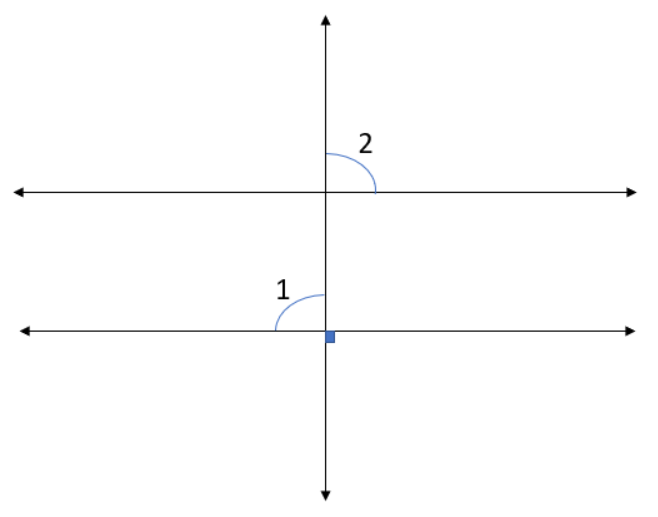
Ans. Two angles are congruent if they are equal in measure, in the following image, the 1st angle, by the vertically opposite angles property, is a right angle. For, the second angle, using the corresponding angles property we can say that the angle adjacent to it is also a right angle. Now using the linear pairs,

\[{90^\circ } + \angle 2 = {180^\circ }\]

\[\angle 2 = {90^\circ }\]

Hence, the 2nd angle is also a right angle. Thus, the two angles are congruent.

Want to dive deeper into the topic of congruence? Check out our article on “Congruence for Triangles“