Properties of Division of Integers

Introduction

Natural numbers, their additive inverses, and zero are all collectively known as a set of integers. We get a whole number when we subtract a small number from a larger number. However, there are no whole numbers that can represent the difference between a large number and a smaller number, such as 12 – 37. We created integers to describe such differences. Integer Addition follows all the rules of algebra, whereas integer subtraction doesn’t.

Division of Integers

We can use the properties of integer division because we are accustomed to working with whole numbers and natural numbers. 

The Division of Integers rules:

Rule 1: A positive integer is always the quotient of two positive integers or two negative integers.

Rule 2: A positive integer’s quotient when divided by a negative integer is always negative.

One important thing to keep in mind is that you should always divide without signs, but once you have the integer solution, give the sign following the sign specified in the problem.

Learn More about Properties of Division of Integers. Check out more videos in Maths Class 7 Lesson no 01.

Properties of Integer Operations

Integers have a few properties that govern how they operate. These principles or properties can be used to solve a wide range of equations. Integers are any positive or negative number, including zero, to refresh your memory. These integers’ properties will aid in quickly simplifying and answering a series of integer operations.

All addition, subtraction, multiplication, and division properties and identities apply to all integers. The set of positive, zero, and negative numbers represented by the letter Z is known as an integer. Integers have the following five operational properties:

• Closure Property
• Commutative Property
• Associative Property
• Distributive Property
• Identity Property

Closure Property

According to the closure property, the set of all integers is closed under addition and multiplication, i.e., addition or multiplication of any two integers will always result in an integer. Subtraction of integers also follows the closure property; division however does not follow the same rule for integers.

If a and b are two integers, then if,

c = a + b and d = a × b

Then both c and d are also integers.

But r = a/b is not always an integer.

Thus, the division of integers is not always closed.

Commutative Property

According to the commutative property of addition and multiplication, the order of terms does not affect the result. Let a and b be two integers, then by the commutative law:

a + b = b + a

Also,

a x b = b x a

But subtraction and Division do not follow the same rules.

Associative Property

According to the associative property of addition and multiplication, it doesn’t matter how numbers are grouped; the result is the same. Regardless of the order of the terms, parenthesis can be used.

a + (b + c) = (a + b) + c

Also,

a × (b × c) = (a × b) × c

However, again subtraction and Division are not associative for Integers.

Distributive Property

The distributive property explains how one mathematical operation can distribute over another within a bracket. To make the calculations easier, the distributive property of addition or the distributive property of subtraction could be used. In this case, integers are multiplied or divided by each number in the bracket before being added or subtracted again.

Multiplication is distributive from both sides, but Division is distributive only from the right side (denominator/divisor)

(a ± b) ÷ c = (a ÷ c) ± (b ÷ c)

Identity Property

When any integer is added to zero no matter the order, the result is the same number, according to the additive identity property of integers. Zero is known as additive identity.

Let a be an integer

Then, since 0 is known as additive identity

a + 0 = a = 0 + a

Similar to this, we have the multiplicative identity. When a number is multiplied by 1 in any order, the product is the integer itself, according to the multiplicative identity property for integers.

Again, let a be an integer,

Then, since 1 is known as the multiplicative identity

a × 1 = a = 1 × a

Again, like most other properties, subtraction and division do not follow the identity property.

BODMAS Rule

To simplify the calculations of more than two numbers having several types of operators, we have formed a rule that governs how to put parentheses around certain terms when solving the parentheses from the centre simplifies the calculation a lot.

This rule goes like

Bracket Of Division Multiplication Addition Subtraction – BODMAS

Here in this definition the ‘Of’ stands for functions such as exponents or square roots. So according to this rule, we put the centre of parentheses or brackets on subtraction, then addition, then multiplication and then division leaving the functions outside.

Solved Examples

Example: Are the following Integer operations closed (have an Integer result)?

a.  2 + 3/ (5 – 2)

b.  4(3/8) + 5/15

Solution:

a.  2 + 3/ (5 – 2)

Using BODMAS, we will simplify the terms by solving within the parentheses first.

⇒ 2 + 3/ (3)

⇒ 2 + 1 = 3

This operation is closed.

b.  4(3/8) + 5/15

Using BODMAS, we will simplify the terms by solving within the parentheses first.

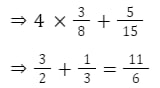
This operation is not closed.

Also Read: Properties of Addition and Subtraction of Integers

Summary

This article discusses the topic of Integers, Integer Division. While also shining a light on the properties of Integers operations such as closure property, commutative property, etc. Integer division however does not follow most of these properties.

FAQs

 1. What are Integers? How are they different from other types of numbers, such as natural numbers and whole numbers?
Ans. Integers are numbers that have no decimal value, they are represented by whole values. The integers contain both positive and negative numbers along with the number 0. The positive integers are known as natural numbers, whereas the positive integers with 0, aka the non-negative integers, are known as whole numbers.

2. What are the rules for Dividing Integers?
Ans. The division of integers follows two simple rules,

1. Dividing two integers of the same sign results in the quotient of the value of those numbers and the result has a positive sign.
2. Dividing two integers of different signs results in the quotient of the value of integers and the result has a negative sign.

3. Which is the only Property of Integer Operations that Division follows, and on What Condition?
Ans. The distributive property is the only property of integer operations that the division of integers follows, and it follows the distributive property only from the right-hand side.