1. Given here are some figures.
Classify each of them on the basis of the following.
(a) Simple curve (b) Simple closed curve (c) Polygon (d) Convex polygon (e) Concave polygon
1. Given here are some figures.
Classify each of them on the basis of the following.
(a) Simple curve (b) Simple closed curve (c) Polygon (d) Convex polygon (e) Concave polygon
Explanation:
a) 1, 2, 5, 6 and 7 are simple curve as they can be drawn without lifting the pencil and they have no overlapping parts.
b) 1, 2, 5, 6 and 7 are simple closed curve as they can be drawn without lifting the pencil and they have no overlapping parts and they are closed figures.
c) 1 and 2 are polygon because they are simple closed curve and they are made by line segments only.
d) 2 is a convex polygon because they are simple closed curve and they are made by line segments only and all interior angles of these curves are less than 180°.
e) 1 is a concave polygon because they are simple closed curve and they are made by line segments only and one or more of interior angles of these curves are greater than 180°.
2. How many diagonals does each of the following have?
a) A convex quadrilateral (b) A regular hexagon (c) A triangle
2. How many diagonals does each of the following have?
a) A convex quadrilateral (b) A regular hexagon (c) A triangle
Explanation:
a) 2 diagonals are present in a convex quadrilateral.
b) 9 diagonals are present in a regular hexagon.
c) There are 0 diagonals in a triangle.
3. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
3. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
Explanation:
Let us consider a convex quadrilateral BCDA as shown above.
The above given quadrilateral is formed from two triangles,
that is, ΔABD and ΔBCD.
As we know, sum of interior angles in a triangle is = 180°.
So, total sum of angles of both the triangle is = 360°, which proves sum of interior angles in a convex quadrilateral is = 360°.
Now, for a non-convex quadrilateral.
Let us consider the quadrilateral is ADCB.
Joining BD, so it divides ADCB into two triangles ΔABD and ΔBDC.
In the ΔABD,
∠β + ∠γ + ∠α = 180° (sum of interior angles in a triangle)
In the ΔBDC,
∠ζ + ∠δ + ∠ε = 180° (sum of interior angles in a triangle)
So, ∠α + ∠β + ∠γ + ∠ζ + ∠δ + ∠ε = 180° + 180°
⇨ ∠α + ∠β + ∠γ + ∠ζ + ∠δ + ∠ε = 360°
Also, ∠C = ∠ε, ∠B = ∠α + ∠γ, ∠A = ∠β, ∠D = ∠γ + ∠δ
⇨ ∠A + ∠D + ∠B + ∠C = 360°.
So, the property still holds true if the quadrilateral is non-convex.
4. Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
What can you say about the angle sum of a convex polygon with number of sides?
(a) 7 (b) 8 (c) 10 (d) n
4. Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
What can you say about the angle sum of a convex polygon with number of sides?
(a) 7 (b) 8 (c) 10 (d) n
Explanation:
As we know,
The sum of interior angles in a polygon with side n = 180°×(n–2).
a) 7
when, n = 7
Then, sum of angles = 180°×(7–2) = 180°×5 = 900°
b) 8
when, n = 8
So, sum of angles = 180°×(8–2) = 180°×6 = 1080°
c) 10
when, n = 10
Then, sum of angles = 180°×(10–2) = 180°×8 = 1440°
d) n
when, n = n
So, sum of angles = 180°×(n–2)
5. What is a regular polygon?
State the name of a regular polygon of
(i) 3 sides (ii) 4 sides (iii) 6 sides
5. What is a regular polygon?
State the name of a regular polygon of
(i) 3 sides (ii) 4 sides (iii) 6 sides
Explanation:
Regular polygon: A polygon is a closed shape whose side lengths are equal and all the angles between adjacent sides are equal. So, A regular polygon is equilateral as well as equiangular. Regular polygons can have any number of sides, but they must have at least three sides.
(i) An equilateral triangle is the only regular polygon with 3 sides since all sides and angles are equal to one another.
(ii) A square is a regular polygon with 4 sides since all sides and angles are equal to one another.
(iii) A hexagon is a regular polygon with 6 sides since all angles and sides are equal to one another.
6. Find the angle measure of x in the following figures.
6. Find the angle measure of x in the following figures.
Explanation:
a) The given figure contains 4 sides. So, it is a quadrilateral.
We know, sum of interior angles in a given quadrilateral is = 360°
So, sum of angles = 360°.
⇨ x + 50° + 120° + 130° = 360°
⇨ x + 300° = 360°
⇨ x = 360° – 300°
⇨ x = 60°.
b) The given figure contains 4 sides. So, it is a quadrilateral and one of the interior angles is given to be 90°.
We know, sum of interior angles in a given quadrilateral is = 360°
So, sum of angles = 360°.
⇨ x + 60° + 90° + 70° = 360°
⇨ x + 220° = 360° (transfer 220° from LHS to RHS)
⇨ x = 360° – 220° (simplify)
⇨ x = 140°.
c) The given figure contains 5 sides. So, it is a pentagon
We know, sum of interior angles of a pentagon = (n–2) × 180° = (5–2)×180° = 3×180° = 540°.
Also, it is given that two angles are equal that is = x
First unknown angle is = 180° – 70° = 110°
Second unknown angle is = 180° – 60° = 120°
⇨ x + x + 30° + 120° + 110° = 540°
⇨ 2x + 260° = 540° (transfer 260° from LHS to RHS)
⇨ 2x = 540° – 260°
⇨ 2x = 280° (divide LHS and RHS by 2)
⇨ x = 140°
d) The given figure contains 5 sides. So, it is a regular pentagon. Hence, all the angles are equal in measurement.
As we know that, sum of interior angles in a pentagon is = (n–2) × 180° = (5–2)×180° = 3×180° = 540°.
x + x + x + x + x = 540°
⇨ 5x = 540° (divide LHS and RHS by 5)
⇨ x = 540°/5 (simplify)
⇨ x = 108°.
7. 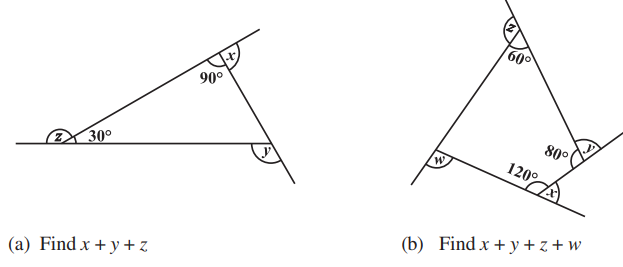
7.
Explanation:
a)As we know that, sum of all interior angles in a triangle is = 180°
Unknown interior angle of the triangle is = 180°– (30° + 90°) = 180° – 120° = 60°
We know, two points on a line are 180° to one another. So,
z + 30° = 180°
⇨ z = 180° – 30°
⇨ z = 150°
y + 60° = 180° (transfer 60° from LHS to RHS)
⇨ y = 180° – 60°
⇨ y = 120°
x + 90° = 180°
⇨ x = 180° – 90°
⇨ x = 90°.
So, z + y + x = 150° + 120° + 90° = 360°
b) we know, sum of all interior angles in a quadrilateral is = 360°. So,
One unknown angle of the quadrilateral = 360°– (120° + 60° + 80°) = 360° – 260° = 100°
We know, two points on a line are 180° to one another. So,
z + 60° = 180°
⇨ z = 180° – 60°
⇨ z = 120°
y + 80° = 180° (transfer 80° from LHS to RHS)
⇨ y = 180° – 80°
⇨ y = 100°
w + 100° = 180° (transfer 100° from LHS to RHS)
⇨ w = 180° – 100°
⇨ w = 80°
x + 120° = 180° (transfer 120° from LHS to RHS)
⇨ x = 180° – 120°
⇨ x = 60°
w + y + x + z = 120° + 100° + 80° + 60° = 360°.
8. Find x in the following figures.
8. Find x in the following figures.
Explanation:
a)
Let us assume the unknown interior angles to be y and z.
The third interior angle will be = 180°– x (two points on a line a 180° apart)
Similarly,
y + 125° = 180° (transfer 125° from LHS to RHS)
⇨ y = 180° – 125°
⇨ y = 55°
z + 125° = 180°
⇨ z = 180° – 125°
⇨ z = 55°
We know the sum of interior angles in a triangle is = 180°. So,
z + y + 180° – x = 180°
⇨ 55° + 55° + 180° – x = 180° (simplify)
⇨ x = 55° + 55°
⇨ x = 110°
Answer- 110°
b)
From the given figure we conclude that, two of the interior angles are = 90°.
Now the other two angles will be
y + 70° = 180° (because of linear pair)
⇨ y = 180° – 70°
⇨ y = 110°
z + 60° = 180° (because of linear pair)
⇨ z = 180° – 60°
⇨ z = 120°
And the fifth angle will be = 180° – x.
The given figure is a pentagon as it has 5 sides.
AS we know that, sum of interior angles in a polygon is = (n – 2)×180° (for a polygon n = 5)
Sum of all the interior angles in the pentagon is = 3×180° = 540°.
⇨ 90° + 120° + 90° + 110° + 180° – x = 540°
⇨ 590° + x = 540°
⇨ x = 590° – 540°
⇨ x = 30°
Answer- 30°
9. Find the measure of each exterior angle of a regular polygon of
(i) 9 sides (ii) 15 sides
9. Find the measure of each exterior angle of a regular polygon of
(i) 9 sides (ii) 15 sides
Explanation:
As we know that, sum of interior angles in a regular polygon with n sides is = (n – 2)×180°
(i) Sum of all the interior angles in a regular polygon with 9 sides is = 180° × (9–2)
= 180°×7
= 1260°
So, each of the interior angle will be = 1260°/9 = 140°
That is, each of the exterior angle will be = 180° – 140° = 40° (due to linear pair)
Also,
Each of the exterior angle = (sum of all exterior angles in the polygon)/(Number of sides of regular polygon)
= 360°/9
= 40°
(ii) Sum of all the interior angles of a regular polygon with 15 sides is = 180°×(15 – 2)
= 180°×13
= 2340°
So, each of the interior angle will be = 2340/15 = 156°
That is, each of the exterior angle will be = 180° – 156° = 24°.
Also,
Each of the exterior angle = (sum of all exterior angles in the polygon)/(Number of sides of regular polygon)
= 360°/15
= 24°
10. How many sides does a regular polygon have if the measure of an exterior angle is 24°?
10. How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Explanation:
As we know,
Each of the exterior angle = (sum of all exterior angles in the polygon)/(Number of sides of regular polygon)
24° = 360°/ Number of sides present in polygon
⇨ Number of sides present in polygon = (360°)/(24°) = 15
Hence, the desired regular polygon contains 15 sides.
11. How many sides does a regular polygon have if each of its interior angles is 165°?
11. How many sides does a regular polygon have if each of its interior angles is 165°?
Explanation:
It has been given that,
Each of the interior angle = 165°
So,
Each of the exterior angle will be = 180° – 165° = 15° (due to linear pair)
We know,
Each of the exterior angle = (sum of all exterior angles in the polygon)/(Number of sides of regular polygon)
⇨ Number of sides present in polygon = 360°/(15°) = 24
Hence, the desired regular polygon contains 24 sides.
12. a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
b) Can it be an interior angle of a regular polygon? Why?
12. a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
b) Can it be an interior angle of a regular polygon? Why?
Explanation:
Solution-
a) It has been given that,
Each of the exterior angle will be = 22°
We know,
Each of the exterior angle = (sum of all exterior angles in the polygon)/(Number of sides of regular polygon)
⇨ Number of sides present in polygon = 360°/(22°) = 16.36
As the number of sides present in the polygon is coming to be 16.36, it is not possible to have a regular polygon. Number of sides is always an integer. For the sides to be an integer, the exterior angle must divide 360°.
Answer- NO.
b) It has been given that,
Each of the present interior angle = 22°
So,
Each of the exterior angle will be = 180° – 22° = 158° (due to linear pair)
We know,
Each of the exterior angle = (sum of all exterior angles in the polygon)/(Number of sides of regular polygon)
⇨ Number of sides present in polygon = 360°/(158°) = 2.2784
As the number of sides present in polygon is coming to be 2.2784, it is not possible to have a regular polygon. The number of sides is always an integer. For the sides to be an integer, the exterior angle must divide 360°.
Answer- NO.
13. a) What is the minimum interior angle possible for a regular polygon? Why?
b) What is the maximum exterior angle possible for a regular polygon?
13. a) What is the minimum interior angle possible for a regular polygon? Why?
b) What is the maximum exterior angle possible for a regular polygon?
Explanation:
a) An equilateral triangle is the only regular polygon with least number of sides possible that is 3 sides. So, the minimum interior angle is possible in Equilateral triangle only.
As we know that,
Sum of the interior angles of a triangle is = 180°
Hence, each of the interior angle is = (180°)/3 = 60°.
b) An equilateral triangle is the only regular polygon with least number of sides possible that is 3 sides. When the interior angle is minimum then external angle will be maximum. So, the maximum exterior angle is possible in Equilateral triangle only.
We know,
Minimum interior angle possible is = 60°
Hence, each of the exterior angle is = 180° – 60° = 120°.
14. Given a parallelogram ABCD. Complete each statement along with the definition or property used.
(i) AD = …… (ii) ∠DCB = ……
(iii) OC = …… (iv) m ∠DAB + m ∠CDA = ……
14. Given a parallelogram ABCD. Complete each statement along with the definition or property used.
(i) AD = …… (ii) ∠DCB = ……
(iii) OC = …… (iv) m ∠DAB + m ∠CDA = ……
Explanation:
(i) AD = BC
Because in parallelograms side opposite to each other are of same length.
(ii) ∠DCB = ∠DAB
Because in parallelograms angle opposite to each other are of same measure.
(iii) OC = OA
Because in parallelograms diagonal are of equal length.
(iv) m ∠DAB + m ∠CDA = 180°
Because in parallelograms sum of adjacent angles are equal to 180°.
15. Consider the following parallelograms. Find the values of the unknown x, y, z
15. Consider the following parallelograms. Find the values of the unknown x, y, z
Explanation:
(i)
As, opposite angle in parallelograms are equal. Hence,
∠B = ∠D = 100° or y = 100° and
∠C = ∠A or x = z
Also, summation of adjacent angles of a parallelogram is = 180°. So,
∠B + ∠C = 180°
100° + x = 180° (transfer 100° from LHS to RHS)
⇨ x = 180° – 100° (simplify)
⇨ x = 80°.
Since, x = z
z = 80°.
∠A + ∠D = 180° (adjacent angle property of parallelogram)
z + y = 180°
⇨ 80° + y = 180° (transfer 80° from LHS to RHS)
⇨ y = 180° – 80°
⇨ y = 100°
Hence, y = 100°, z = 80° and x = 80°.
(ii)
Using adjacent angle property of parallelogram
x + 50° = 180° (transfer 50° from LHS to RHS)
⇨ x = 180° – 50° (simplify)
⇨ x = 130°.
As, angles opposite to one another in parallelogram are equal
y = x = 130°.
x + (180° – z) = 180° (adjacent angle property of parallelogram)
x = z = 130°.
Answer- z = 130°, y = 130°, x = 130°.
(iii)
From figure, using vertically opposite angle property
x = 90°
y + x + 30° = 180° (property of sum of internal angles of a triangle)
⇨ y + 90° + 30° = 180°
⇨ 120° + y = 180° (transfer 120° from LHS to RHS)
⇨ y = 180° – 120° (simplify)
⇨ y = 60°.
From alternate angles property
z = y = 60°.
(iv)
In above parallelogram,
z = 80° (property of corresponding angle in a parallelogram)
y = z = 80° (angles alternate to one another are equal in parallelogram)
y + x = 180° (sum of angles adjacent to one another are equal to 180°)
⇨ 80° + x = 180°
⇨ x = 180° – 80°
⇨ x = 100°
(v)
In the above parallelogram,
y = 112° (opposite angle property of parallelogram)
Also, 40° + y + x = 180° (sum of interior angles of a triangle equals to 180°)
⇨ 40° + 112° + x = 180°
⇨ 152° + x =180° (transfer 152° from LHS to RHS)
⇨ x = 180° – 152° (simplify)
⇨ x = 28°.
From property of alternate angles,
z = x = 28°.
So, x = 28°, z = 28°, y = 112°.
16. Can a quadrilateral ABCD be a parallelogram if (i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii)∠A = 70° and ∠C = 65°?
16. Can a quadrilateral ABCD be a parallelogram if (i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii)∠A = 70° and ∠C = 65°?
Explanation:
(i) A quadrilateral ABCD can be qualified to be a parallelogram if ∠D + ∠B = 180° and the below given conditions are also satisfied:
(a) Summation of adjacent angles of the quadrilateral is = 180°.
(b) Opposite angles of the quadrilateral must be equal.
(ii) No, here AD ≠ BC. Opposite sides must be of equal length to be parallelogram.
(iii) No, here ∠A ≠ ∠C. Opposite angles must be equal in measurement to be a parallelogram.
17. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
17. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Explanation:
The figure of quadrilateral is drawn above. It has two equally opposite angles, ∠D = ∠B. But ∠C ≠ ∠A, so it is not considered as parallelogram. Also, parallelogram has equally opposite sides.
18. The measures of two adjacent angles of a parallelogram are in the ratio 3:2. Find the measure of each of the angles of the parallelogram.
18. The measures of two adjacent angles of a parallelogram are in the ratio 3:2. Find the measure of each of the angles of the parallelogram.
Explanation:
Let the measure of ∠A is = 3x
and let the measure of ∠B is = 2x so their ratio remains 3:2 in a parallelogram named ABCD.
As, these two angles are adjacent to one another and they are angles of a parallelogram. Hence, there sum must be equal to 180°.
∠B + ∠A = 180°
⇨ 2x + 3x = 180° (putting the values of angles)
⇨ 5x = 180° (divide LHS and RHS by 5)
⇨ x = 180°/5.
⇨ x= 36°.
So, ∠A = 3x
⇨ ∠A = 3×36°
⇨ ∠A = 108°.
And ∠B = 2x
⇨ ∠B = 2×36°
⇨ ∠B = 72°.
As opposite angles are equal in measure in a parallelogram. So,
∠C = ∠A = 108°
∠D = ∠B = 72°.
19. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
19. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Explanation:
Let ∠A and ∠D are equal in parallelogram ABCD (given in the question)
Let ∠A = ∠D = x
We know, sum of angles adjacent to one another in a parallelogram is = 180°
∠D + ∠A = 180°
⇨ x + x = 180°
⇨ 2x = 180° (divide LHS and RHS by 2)
⇨ x = 90°
So, ∠A = ∠D = x = 90°
Also, ∠C + ∠D = 180°
⇨ ∠C + 90° = 180° (transfer 90° from LHS to RHS)
⇨ ∠C = 90°.
Similarly, ∠C + ∠B = 180°.
⇨ ∠B + 90° = 180° (transfer 90° from LHS to RHS)
⇨ ∠B = 180° – 90°
⇨ ∠B = 90°.
20. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
20. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
Explanation:
From figure, Internal ∠O = 180° – 70°
∠O = 110°.
Also, ∠H + ∠O = 180° (adjacent angle sum property)
⇨ z + 40° + 110° = 180°
⇨ z + 150° = 180° (transfer 150° from LHS to RHS)
⇨ z = 180° – 150° (simplify)
⇨ z = 30°.
Also, ∠E = ∠O (opposite angle property)
⇨ x = 110°.
Now, in triangle HOP. Summation of all interior angles must be equal to 180°.
So, y + z + ∠O = 180°
⇨ 30° + y + 110° = 180°
⇨ y + 140° = 180° (transfer 140° from LHS to RHS)
⇨ y = 180° – 140° (simplify)
⇨ y = 40°.
Answers- x = 110°, y = 40°, z= 30°
The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
Explanation:
(i) In a parallelogram side opposite to each other are of equal lengths. So,
SN = GU and SG = NU
⇨ 3y – 1 = 26 (transfer –1 from LHS to RHS)
⇨ 3y = 26 + 1
⇨ 3y = 27 (divide LHS and RHS by 3)
⇨ y = 27/3 (simplify)
⇨ y = 9
Now, SG = NU
⇨ 3x = 18 (divide LHS and RHS by 3)
⇨ x = 18/3 (simplify)
⇨ x = 6
Answer- x = 6, y = 9.
(ii) In a parallelogram diagonal bisect each other. So,
16 = x + y and 20 = y + 7
⇨ y + 7 = 20 (transfer 7 from LHS to RHS)
⇨ y = 20 – 7 (simplify)
⇨ y = 13
Now,
⇨ x + y = 16
⇨ x + 13 = 16 (transfer 13 from LHS to RHS)
⇨ x = 16 – 13 (simplify)
⇨ x = 3
Answer- x = 3, y = 13
22. In the above figure both RISK and CLUE are parallelograms. Find the value of x.
22. In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Explanation:
From adjacent angle property in parallelogram KRIS
∠R + ∠K = 180°
⇨ ∠R + 120° = 180° (transfer 120° from LHS to RHS)
⇨ ∠R = 180° – 120°
⇨ ∠R = 60°.
From property of corresponding angles
∠SIL = ∠R
⇨ ∠SIL = 60°
From property of corresponding angles
∠ECR = ∠L
∠ECR = 70°
As summation of all the interior angles of a triangle is = 180°. So, in the small triangle with base IC
x + ∠ECR + ∠SIL = 180°
⇨ x + 70° + 60° = 180°
⇨ x + 130° = 180° (transfer 130° from LHS to RHS)
⇨ x = 180° – 130° (simplify)
⇨ x = 50°.
23. Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
23. Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
Explanation:
When a transversal intersects two lines, if the adjacent angles on the same side of the transversal adds up to 180°, then these two lines are said to be parallel lines. In this figure,
∠M + ∠L = 100° + 80°
∠M + ∠L = 180°.
Hence, MN || LK (MN is parallel to LK)
Since the given quadrilateral LMNK contains one pair of parallel line, the above given figure can be said to be a trapezium. The two parallel lines are MN and LK.
24. Find m∠C in Fig 3.33 if AB || DC.
24. Find m∠C in Fig 3.33 if AB || DC.
Explanation:
It has been given that AB || DC. From the property of angle on same side of transversal line, there angle sum must be equal to 180°. So,
m∠B + m∠C = 180°
⇨ 120° + m∠C = 180° (transfer 120° from LHS to RHS)
⇨ m∠C = 180° – 120° (simplify)
⇨ m∠C = 60°.
Answer- 60°.
25. Find the measure of ∠P and ∠S if SP || RQ? in Fig 3.34. (If you find m∠R, is there more than one method to find m∠P?)
25. Find the measure of ∠P and ∠S if SP || RQ? in Fig 3.34. (If you find m∠R, is there more than one method to find m∠P?)
Explanation:
It has been given that SP || RQ. From the property of angle on same side of transversal line, there angle sum must be equal to 180°. So,
∠Q + ∠P = 180°
⇨ 130° + ∠P = 180° (transfer 130° from LHS to RHS)
⇨ ∠P = 180° – 130° (simplify)
⇨ ∠P = 50°
Similarly,
∠S + ∠R = 180°
⇨ ∠S + 90° = 180° (transfer 90° from LHS to RHS)
⇨ ∠S = 180° – 90° (simplify)
⇨ ∠S = 90°
Hence, ∠S = 90° and ∠P = 50°.
Yes, there can be more than one way of finding m∠P.
A quadrilateral QRSP is given. Sum of measures of all the interior angles is = 360°.
And, ∠R = 90°, ∠S = 90° and ∠Q = 130°
90° + 130° + 90° + ∠P = 360°
⇨ ∠P + 310° = 360° (transfer 310° from LHS to RHS)
⇨ ∠P = 360° – 310° (simplify)
⇨ ∠P = 50°
26. State whether True or False.
(a) All rectangles are squares.
(b) All rhombuses are parallelograms.
(c) All squares are rhombuses and also rectangles.
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
26. State whether True or False.
(a) All rectangles are squares.
(b) All rhombuses are parallelograms.
(c) All squares are rhombuses and also rectangles.
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
Explanation:
(a) False
In squares all side are of equal lengths but in rectangles opposite sides are of equal lengths.
(b) True
All rhombuses are parallelograms because the sides that are opposite to each other are also parallel to each other.
(c) True
All squares are rhombuses because they have equal length sides and diagonals are at right angles. All squares are rectangles because all angles are at right angles to each other.
(d) False
All squares are not parallelograms because they do not have both pairs of opposite sides parallel to one another.
(e) False.
All rhombuses are not kites because kites contain two pairs of adjacent congruent sides while in rhombuses all sides are congruent.
(f) True
All rhombuses are kites because they have two pairs of adjacent sides and they are congruent.
(g) True
All parallelograms are trapeziums because they have at least one pair of sides that are parallel.
(h) True
All squares are trapeziums because they have at least one pair of sides that are parallel.
27. Explain how a square is
(i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle
27. Explain how a square is
(i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle
Explanation:
(i) Square are also quadrilaterals because it contains four sides. In square all sides are of same length.
(ii) Squares are also parallelograms because the angles opposite to one another are equal and the opposite sides are parallel.
(iii) Squares are also rhombuses because the diagonals bisect 90°and all four sides contain same length.
(iv) Squares are also rectangle because all the interior angles of the square are equal to 90°.



